Module Components

• Overview

Topics

• Partial Correlation
• Modeling Independent Variables in Regression Models
• Multiple Linear Regression
• Multiple Logistic Regression

NRSG 795: BIOSTATISTICS FOR EVIDENCE-BASED PRACTICE

Module 9: Model Building-Multiple Independent Variables

Partial Correlation

Partial correlation is an extension of the Pearson correlation where the effect of a third variable is statistically controlled. If you think of a Venn Diagram that represents the correlation between two variables, the intersection represents the amount of variation that is shared between the two variables. In the example below, assume that we hypothesize that there is a relationship between hours worked and hours exercised. But we know that age influences both so we want to “control” for age.

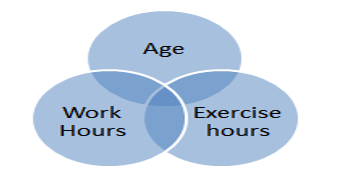
The overlap of the work and exercise circles represents the correlation between the two variables (a zero order correlation).  When age is included, you can see that age is correlated with both hours of work and hours of exercise since it overlaps both.  In partial correlation, the overlap between work and exercise is measured while controlling for age i.e., removing the effect of age. Think of erasing the circle for age and then you would see that the area of shared variation between work hours and exercise hours changes.

Partial correlation is used when there are only a few variables or when there are a limited number of observations (N<30).  If there are more variables and more observations, a linear regression can be used to do this same analysis. Thinking of the Venn Diagram example, adding a 3rd, 4th, and 5th variable to the model would be reflected in adding 3 more circles, where the amount of overlap among the variables varies.  This is a good way to think about linear regression, where we look at the simultaneous impact of a set of variables on a single dependent variable.

Required Videos

• Partial correlation tutorial (9:29)
  Note that this spends several minutes on how to report partial correlations