Module Components

• Overview

Topics

• Significance Testing and Hypothesis Testing
• Type I and Type II Errors
• Effect Size
• Sample Size

NRSG 795: BIOSTATISTICS FOR EVIDENCE-BASED PRACTICE

Module 4: Inferential Statistics

Significance Testing and Hypothesis Testing

Statistical hypothesis testing provides objective decisions about whether study results likely reflect chance sample differences or true population differences (click here for an overview of the sequential steps involved in hypothesis testing).

First, define a threshold p-value before you do the experiment. Ideally, you should set this value based on the relative consequences of missing a true difference or falsely finding a difference. In practice, the threshold value (called alpha) is almost always set to 0.05 (an arbitrary value that has been widely adopted).

Next, define the null hypothesis. If you are comparing two means, the null hypothesis is that the two populations have the same mean. When analyzing an experiment, the null hypothesis is usually the opposite of the experimental hypothesis. Your experimental hypothesis -- the reason you did the experiment -- is that the treatment changes the mean. The null hypothesis is that two populations have the same mean (or that the treatment has no effect).

Now, perform the appropriate statistical test to compute the p-value.

• If the p-value is less than the threshold, state that you “reject the null hypothesis” and that the difference is “statistically significant”.
• If the p-value is greater than the threshold, state that you “do not reject the null hypothesis” and that the difference is “not statistically significant”. You cannot conclude that the null hypothesis is true. All you can do is conclude that you don't have sufficient evidence to reject the null hypothesis.

The significance level or alpha is equal to the percentage chance that the null hypothesis is rejected when in actuality it is true.

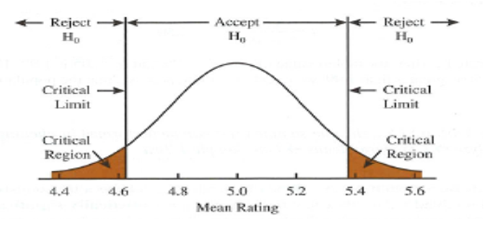
The figure below provides a graphic for what is happening in a two tailed test. When you perform a statistical test the value of the computed statistic is compared to what would be expected by chance alone. The alpha level defines ‘the chance alone’. The range of values in which the null hypothesis is rejected is called the ‘critical region’ and the cutoff values at which the null hypothesis is rejected are the threshold or ‘critical values’. In the figure below, the null hypothesis assumes a population mean of 5 and 95% of all sample means fall between 4.6 and 5.4 (within 2 SD above and below mean). If our sample mean is 7.1 we see this lies in the critical region (above the threshold) which indicates improbable support for the null hypothesis being correct. We conclude we cannot accept the null hypothesis and must instead accept the alternative hypothesis (a corresponding p-value for the sample mean of 7.1 would show a value <.05).

In statistics significant means the results are not likely to have been a result of chance at a specified level of probability.

Results that are statistically significant are not necessarily clinically significant. Clinically significant differences imply differences large enough to indicate a preferential clinical approach or course of treatment. A result must be statistically significant AND clinically useful in order to be clinically significant.

One-tailed Versus Two-tailed Tests

In general, for most situations researchers use two-tailed tests. A two-tailed test is one that uses both tails of the distribution to determine the critical region for rejecting the null hypothesis. The hypothesis states that there may be a difference or an association but it doesn’t specify a direction, such as expressing the difference as an increase/decrease or a positive/negative association. One can think of this as the conservative view in something like an intervention cause not all interventions work out as you hope to always show improvement (sometimes the placebo group is far better off). Our area of 5% improbable values is split in half so that 2.5% is at the lower end and 2.5% is at the higher end of the distribution (as shown in the figure above). Most software packages provide two-tailed values as the default.

EXAMPLE: Null hypothesis: The average number of falls in two different nursing homes (A&B) is equal. Alternative hypothesis: The average number of falls is different for nursing home A from nursing home B. Since the hypothesis does not mention if the average number of falls in home A is higher or lower than home B this would be a non directional hypotheses and one would use a two-tailed test.

On the other hand, sometimes the two-tailed test is too conservative. If the researcher has a strong basis for predicting a specific direction for the alternative hypothesis, a one-tailed test may be appropriate. In a one-tailed test, the critical region is entirely in one tail of the distribution. It is easier to reject the null hypothesis because the entire 5% of improbable values are at one end.

EXAMPLE: Null hypothesis: The average number of falls in two different nursing homes (A&B) is equal. Alternative hypothesis: The average number of falls in nursing home A is less than the average number of falls in nursing home B. Since we are hypothesizing a direction in the difference (# falls in home A<home B) this would be a directional hypotheses and one could use a one-tailed test.

In research reports, unless it is stated assume a two-tailed test was performed. As pointed out, it is a conservative approach and the risk of committing a Type I error is reduced (next topic). The decision to use a one-tailed test should always be based on theory or prior research evidence that strongly suggests that findings in the opposite direction to that proposed are virtually impossible. The decision should be made prior to performing any analyses and not changed after seeing the result.

Required Readings

• Understanding the p-value (4:42) http://www.youtube.com/watch?v=eyknGvncKLw
• Hypothesis tests, p-values – statistics help (7:37) http://www.youtube.com/watch?v=0zZYBALbZgg&list=PLm9FYjKtq7Pzjh7e727hSr8VvSR9OvqsZ
• NOT REQUIRED: article with more information

Learning Activity

For the statements below determine

• What type of hypothesis is this—null or alternative?
• What is the dependent (outcome) variable?
• What is the independent variable?
• What is the level of measure for the dependent variable?

1. The average (mean) loss of body weight of people who exercise is greater than the average (mean) loss of body weight of people who do not exercise.
2. There is no difference between aPTT time (seconds) as measured by the CoaguCheck point-of-care assay and standard laboratory hospital assay for groups of subjects receiving heparin alone, heparin with warfarin, and warfarin and exoenoxaparin. 
3. There is an association between children ED visit per year (Y/N) with food allergies compared to those with insect sting allergies. 

Check your responses here.

Module Components - Overview
Topics - Significance Testing and Hypothesis Testing | Type I and Type II Errors | Effect Size | Sample Size