Module Components

• Overview

Topics

• Significance Testing and Hypothesis Testing
• Type I and Type II Errors
• Effect Size
• Sample Size

NRSG 795: BIOSTATISTICS FOR EVIDENCE-BASED PRACTICE

Module 4: Inferential Statistics

Effect Size

Much of the research in health care has been conceptualized in terms of null hypothesis significance testing (NHST), with a great reliance on the p-values. This approach is increasingly criticized as it reduces relationships being tested (e.g., mean differences, Pearson correlation) to simple reject or not reject testing. Moreover, the p-value calculation is dependent on sample size so large sample sizes may be statistically significant even though the magnitude of the effect is small. Over the last decade, it has become increasingly common to also report effect sizes to help the reader understand the magnitude of the effect being examined. 'Effect size' is simply a way of quantifying the size of the difference between two groups. It is easy to calculate and readily understood.

Why do we need it?

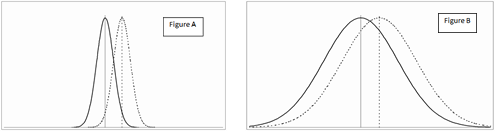
In many studies there often is no familiar scale available on which to record the outcomes to be able to judge if any difference is meaningful. The researcher then has to invent a scale or to use (or adapt) an already existing one - but generally not one whose interpretation will be familiar to most people. One way to get over this problem is to use the amount of variation in scores to contextualise the difference. If there was essentially no overlap at all (figure A) then this would seem like a very substantial difference. On the other hand, if the spread of scores were large and the overlap much bigger than the difference between the groups (figure B), then the effect might seem less significant. Because we have an idea of the amount of variation, we can use this to compare the difference. This idea is quantified in the calculation of the effect size.

Effect sizes have also become more common as the importance of synthesizing research -- across different studies but asking the same question -- has been recognized. One of the main advantages of using effect size is that when a particular experiment has been replicated, the different effect size estimates from each study can easily be combined to give an overall best estimate of the size of the effect.  Systematic reviews may report effect sizes in the evidence summary tables. When effect sizes are analyzed across studies to get a more accurate estimate of the effect in the population, this is called a meta-analysis (module 10).

Effect sizes are also important as they are one of the required metrics to determine the sample size needed to conduct a study (i.e., a power analysis). While a statistician may be consulted or an on-line power calculator may be used in proposing a study, it is the investigator’s responsibility to specify the effect size from the literature or preliminary data. This may require calculating an effect size from data reported in tables or in the text of published studies.

Effect sizes

• are important for EBP as provides a common metric for summarizing evidence in meta analysis
• are a measure of the strength of the relationship between variables
• are an index of how wrong the null hypothesis is
• eliminates dependence on p-values (reject/accept & influence of sample size)

How is it calculated and interpreted(using example of differences between two groups)?

If it is not obvious which of two groups is the 'experimental' (i.e. the one which was given the 'new' treatment being tested) and which the 'control' (the one given the 'standard' treatment - or no treatment - for comparison), the difference can still be calculated. In this case, the 'effect size' simply measures the difference between them, so it is important in quoting the effect size to say which way round the calculation was done.

The 'standard deviation' is a measure of the spread of a set of values. Here it refers to the standard deviation of the population from which the different treatment groups were taken. In practice, however, this is almost never known, so it must be estimated either from the standard deviation of the control group, or from a 'pooled' value from both groups.

An effect size is exactly equivalent to a 'Z-score' of a standard Normal distribution. For example, an effect size of 0.8 means that the score of the average person in the experimental group is 0.8 standard deviations above the average person in the control group, and hence exceeds the scores of 79% of the control group. A score of 0 represents no change and effect size scores can be negative or positive.

The meaning of an effect size varies and is dependent on the measurement context, so rules of thumb should be treated cautiously. A well-known guide is offered by Cohen (1988) to judge standardized mean effect sizes:

Many statistical techniques already are effect sizes – they represent a standardized way to calculate the magnitude of a relationship. For example, a Pearson’s correlation coefficient and odds ratio/relative risk are already “standardized” to a common metric. These tests do not report the results in terms of the actual measure (e.g., weight in pounds, depression measured by the Beck Depression Inventory), rather they remove the actual measure metric and report in a standardized metric (e.g., Pearson r ranges from -1 to 1 and its effect size is from 0 to 1 since effect size measures magnitude, not direction, and thus absolute value of Pearson r). However, other statistical tests need to have an effect size calculated from the reported information. For example, for t-tests the calculated t-value is not an effect size, rather a calculation must be done.

A Cohen’s d (d stands for difference) is a formula that gives a standardized effect size that represents the standardized difference between two means.

The effect size index is different for different statistical tests:

Required Readings

• Effect Size (20:52) https://www.youtube.com/watch?v=rL32SjaHq2A
• Read Using Effect Size-or why the P value is not enough