Module Components

• Overview

Topics

• Sampling Error and Variation
• The Normal Distribution
• Estimating Population Values from Samples

NRSG 795: BIOSTATISTICS FOR EVIDENCE-BASED PRACTICE

Module 3: Variation and the Normal Distribution

Estimating Population Values from Samples

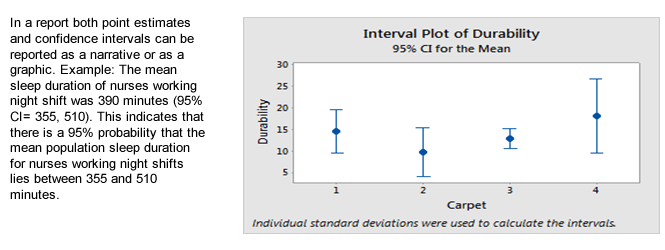
In this section we learn to estimate a population value from the sample (click for more information).

Confidence Intervals

A point estimation involves calculating a single statistic for estimating the parameter. However, point estimates do not give you a context for interpreting their accuracy. In order to overcome this issue, an interval estimation can be performed which gives a range of values that has a high probability of containing the true population value. This is commonly referred to as a confidence interval. Within EBP context, CI is used as means for appraising the evidence, i.e. the  precision of the estimate of effects.

Confidence intervals can be computed around any point estimate such as a mean, percentage, or risk index. For example the 95% CI around a sample mean [point estimate] can be calculated using the formula CI 95% = (Mean ± 1.96 * SD) but this should not be confused with calculating the confidence interval for a population value [parameter estimate]. The problem with point estimates is they are simply descriptive stats and offer no context for interpreting their accuracy. So instead we prefer to estimate a range of values that has a high probability of containing the population value. In order to do that we first must estimate the standard error of the mean.

Standard error of the mean

Standard Error is essentially a standard deviation of a population. A standard error of the mean (SEM) is the standard deviation (SD) of a sampling distribution of the mean. It represents the error expected when the mean from a small sample is used to calculate the SD of the population mean. The term error is used to show that there is sampling error or that the sample means contain some degree of error in estimating the population mean. The term ‘standard’ means that it is a measure of the average amount of error for all possible sample means. Since most sampling distributions are approximately normal, the SEM can be used to estimate the probability of getting a sample mean in a particular range.

SEM= SD/√N

Remember that 95% of the values in a normal distribution lie within + 2 SDs of the mean; so the probability is .95 that a particular mean will be between the two values at +2SD and -2SD. With information about the SEM, sample means can be interpreted relative to the population mean. When the SEM is smaller, there is greater confidence in the estimates of the population value.

CI 95% = (Mean ± 1.96 *SEM)       CI 99% = ( Mean ± 2.58 *SEM)

Since the formula for SEM contains the square root of the population (square root of N) in the denominator, a larger sample size increases the probability that the sample mean will be close to the population mean. In order to decrease the SEM, researchers can increase the sample size. The formula for SEM also has standard deviation (SD) as the numerator, so the smaller the SD (or the greater the homogeneity) of the sample, the smaller is the SEM.

Required Videos

• Central Limit Theorem video (9:48)
• Understanding Confidence Intervals (4:02)
• Calculating the Confidence Interval for a Mean (5:28)
• NOT REQUIRED: article with more information

Learning Activity

• Complete these problems and check your answers here .
• Complete self test 3