Module Components

• Overview

Topics

• Sampling Error and Variation
• The Normal Distribution
• Estimating Population Values from Samples

NRSG 795: BIOSTATISTICS FOR EVIDENCE-BASED PRACTICE

Module 3: Variation and the Normal Distribution

Sampling Error and Variation

While this class focuses on statistics, aspects of the research design are intimately tied to the research questions that can be asked and the statistics that are required to answer those questions.

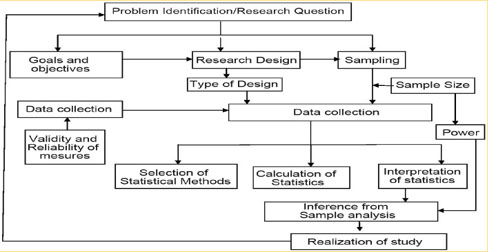
Of particular importance are the measures that are used and the sampling approach. Reliable and valid measures are needed to represent the phenomena of interest (module 10). Furthermore, there must be some variation in the values of what you are assessing to adequately estimate parameters. Likewise, the sampling strategy that is used must adequately represent the population to which you want to generalize your findings. Sampling is the process to select cases to represent an entire population. The sample is a subset of population elements as often the population to be studied is too large to collect data on everyone. Sampling saves time and resources while accurately tracking performance. Thus a sampling strategy is developed that establishes sampling criteria and a sampling methodology to select the study sample. The goal is to be able to generalize the findings from the sample to the population. In clinical research, the population is often an accessible population (the cases that conform to the criteria that are assessable for a study). This is different from a target population which is the aggregate of all cases the researcher would like to generalize the findings to. For example, a target population might consist of all the people with asthma in the US, but the accessible population would be all the people with asthma who attend a particular health clinic.

Sampling methods (selecting the sample)

Representative or Random Sampling Techniques (Probability Sampling)

In order to get a representative sample of the population you need to draw a sample in a systematic way, so that each and every individual has an equal chance of being selected. In these kinds of sampling approaches, a small quantity of a targeted group represents as accurately as possible the entire group. A random sample reduces the chances of bias in the study and increases external validity or generalization of the results.

• Simple random sampling (SRS) – one must have access to every member of the population. Often this is not feasible for large populations, as every person in the population needs to be listed and numbered. Once a complete list is made, the sample is obtained by selecting random numbers and identifying the individuals who correspond to the randomly selected numbers.
• Systematic random sampling - selecting subjects according to a standardized rule- fixed time or count intervals. Begin with a list of the population as a whole and number them. Pick a random number as a starting point and another for the selection number. Then begin with the person corresponding to the starting number chosen and then select every nth person based on your selection number. When using this approach you want to make sure your list does not have any ranked order embedded in it.
• Stratified sampling – the population is divided into subsamples based on characteristics of interest (strata) and then samples are randomly selected from the subgroups. This ensures representativeness of the characteristic.
• Cluster sampling- the population is divided into groups or clusters. Clusters are then chosen at random and all units within the cluster are part of the sample. This approach is often used when the population is scattered over a large geographical area.

Non-representative Sampling Techniques

Non-representative samples are limited with regards to generalization. If a sample is not representative of the population, we cannot make valid inferences about the group from which the sample was drawn.

• Purposive sampling – sample is selected for a specific purpose
• Convenience sampling – using cases you can get, however, volunteers may not be representative of the entire population.
• Snowball (network) sampling – Early members recruited (referred to as seeds) are asked to refer other people. Respondent-driven sampling is a variant of this type of approach often used for sampling hidden populations such as the homeless. 

Sampling criteria (determining eligibility) –a list of requirements or characteristics essential for membership in the target population.

• Inclusion/eligibility criteria – requirements identified that must be present or met for a person to be included in the sample
• Exclusion criteria – requirements identified that eliminate or exclude a person from being in sample.

Specific sampling criteria promotes a smaller, more homogeneous sample. Specifications should be driven by theoretical consideration. The criteria used have implications for the interpretation of the results and the external validity of the findings. Here are some common considerations that influence the criteria:

• Cost: Excluding because of language. Often non-English speaking people are excluded not because the researcher is not interested in them, but the costs of interpreters and setting up a multilingual data collection is cost prohibited.
• Practical constraints: geography/residential status can make it difficult to include people from rural areas
• Health conditions: Mobility, hearing or sight impairment may make it more difficult to participate. Those with mental impairments, in a coma, or in an unstable medical condition may need to be excluded.
• Design consideration: availability in the future- if going to move will you be able to follow them up in your longitudinal study? Focusing on a homogeneous population could be a means of controlling confounding variables.

Sampling for Healthcare Improvement

In quality improvement initiatives, one is aware that data is being collected at the same time as ongoing care is being provided to patients in the community. The environment during an improvement project can be very different from that of a research project, as it focuses on the ongoing process being sampled over time. Therefore, other aspects influence the sample, such as

• The selection of the most appropriate samples are guided by experts in the subject matter
• Past experiences guide the decision if enough data has been obtained

Instead of measuring the entire process (e.g., all patients waiting in the clinic during a month, all ICU transfers) measuring a sample (e.g., every sixth patient for a week, the next ten patients) is a simple, efficient way to help a team understand how a system is performing.

• Systematic sampling - collecting data at fixed time or count intervals — for example, every hour on the hour, or every fourth patient. Systematic sampling is useful for a high-volume process over extended periods of time.

• Block sampling - selecting sample units in a block of predetermined size- for example, measure a straight sequence within a limited time frame.

In summary, findings obtained from samples are used to try to understand what is happening in a population. It is often the case we cannot obtain measurements on the entire population, so instead we rely on data from a select group, hopefully randomly selected. But what is the chance that we obtain the exact point estimate of the mean of the population? The sample statistic is unequal to the corresponding population parameter because of sampling error. Sampling error reflects the tendency for statistics to fluctuate from one sample to another.  One can estimate the error and this is known as the margin of error. The formula for the margin of error is 1/√n, where n is the size of the sample. For example, a random sample of 1,000 has about a 1/√n; = 3.2% error. In general, the larger the sample, the smaller the margin of error.

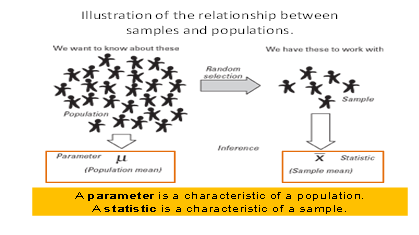
Statistic symbols (and formulas) vary depending on whether one is describing a sample or a population. Here are a few examples

N population size : n sample size
μ Population mean :  x_bar sample mean
ơ2 population variance : s2 sample variance
ơ population standard deviation : s sample standard deviation

Required Videos

• Variation and Sampling Error (6:29)